Machine Learning Homework

1

(1)

$k_1$ and $k_2$ are kernel functions, Mercer Theorm: $K_1$ and $K_2$ are positive semidefinte:

$\forall x\in \mathbb{X} = \{x_1,\ldots, x_N\}, x^TK_i x > 0 ,\;i=1,2$
therefore:
$\forall x \in \mathbb{X}: $

$$\begin{aligned}x^T K_3 x &= x^T(a_1K_1+a_2K_2)x\\ &= a_1 x^TK_1x+a_2 x^TK_2x\geq 0 \end{aligned}$$

Using Mercer theorm, $k_3$ is a kernel function.

(2)

assume $f(X)=[f(x_1),\ldots,f(x_N)]$

$$x^TK_4x = x^Tf(X)^Tf(X)x = (f(X)x)^Tf(X)x \geq 0$$

therefore $k_4$ is a positive definite kernel function.

2

模型序号	模型	偏差	方差
（1）	在线性回归模型中增加权重的正则化项	增大	减小
（2）	对决策树进行剪枝处理	增大	减小
（3）	增加神经网络中隐含层节点的个数	减少	增加
（4）	去除支持向量机中所有的非支持向量	不变	不变

3

(1)

$$\min_{w,b,\xi_i}\; \frac{1}{2} \|w\|^2 +C \sum_{i=1}^{\tilde m}\xi_i +Ck \sum_{i=\tilde m+1}^m \xi_i\\ \begin{aligned} \text{subject to} \quad &y_i(w^Tx_i+b)\geq 1-\xi_i \\&\xi_i \geq 0,\; i=1,\ldots, m\end{aligned}$$

其中 $i = 1,\ldots,\tilde m$ 为正例，$i = \tilde m+1,\ldots, m$ 为反例。

(2)

Lagranian:

$$L(w,b,\alpha, \xi , \mu) = \frac{1}{2} \|w\|^2 +C \sum_{i=1}^{\tilde m}\xi_i +Ck \sum_{i=\tilde m+1}^m \xi_i +\sum_{i=1}^m \alpha_i (1-\xi_i - y_i(w^Tx_i+b))- \sum_{i=1}^m\mu_i\xi_i$$

$\frac{\partial L}{\partial w}=0,\; \frac{\partial L}{\partial b}=0,\;\frac{\partial L}{\partial \xi_i}=0$

$$\begin{aligned} w &=\sum_{i=1}^m \alpha_i y_i x_i\\ 0 &=\sum_{i=1}^m\alpha_i y_i\\ C &= \alpha_i +\mu_i & i =1,\ldots,\tilde{m}\\ kC &= \alpha_i +\mu_i & i =\tilde{m}+1,\ldots,m \end{aligned}$$

dual problem:

$$\max _\alpha \sum_{i=1}^m\alpha_i -\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m \alpha_i\alpha_j y_i y_j x_i^T x_j\\ \begin{aligned} \text{subject to}\quad & \sum_{i=1}^m\alpha_i y_i = 0\\ & 0\leq \alpha_i\leq C,\quad i = 1,\ldots, \tilde{m}\\ & 0\leq \alpha_i\leq kC,\quad i = \tilde{m}+1,\ldots, m\\ \end{aligned}$$

KKT:

$$\begin{array}{l} \alpha_i \geq 0, \quad \mu_i \geq 0 \\ y_i f(x_i) - 1 + \xi_i \geq 0 \\ \alpha_i (y_i f(x_i) - 1 + \xi_i) = 0 \\ \xi_i \geq 0, \quad \mu_i \xi_i = 0 \end{array}$$

4

(1)

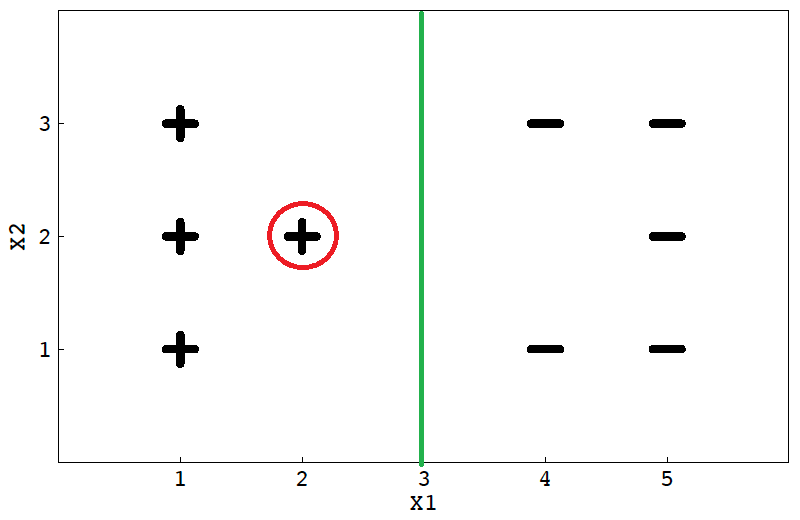
将在 $x_1 =3$直线上，$C$很大的时候对错误的容忍度降低，将会强制划分。

(2)

去掉 $x_1 = 2$ 或者$x_1 = 4$ 上的任一点都会得到新的决策边界，因为它距离边界很近，对边界影响很大。

(3)

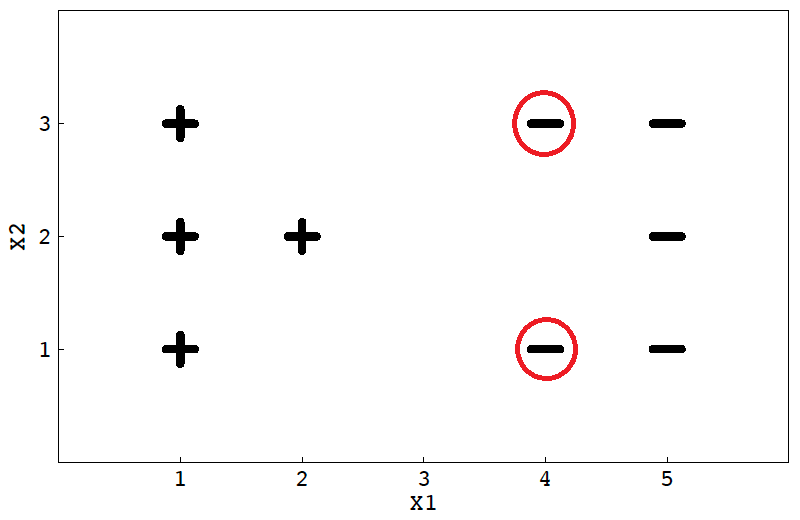
同样的，在边界附近的点对边界影响很大。

(4)

1. 使用3中不同的惩罚系数。
2. 对样本预处理，欠采样；如对多一部分做剔除；过采样；对少的一部分做插值等。
3. 忽略部分非支持向量，保证支持向量数量尽可能的一致。

(5)

$$\begin{aligned} \|\phi(x)-\phi(z)\| &= \sqrt{<\phi(x)-\phi(z),\phi(x)-\phi(z)>}\\ &=\sqrt{<\phi(x),\phi(x)> + <\phi(z),\phi(z)> -2<\phi(x),\phi(z)>}\\ &=\sqrt{K(x,x)+K(z,z)-2K(x,z)} \end{aligned}$$

5

$$f(x|\theta) = \begin{cases} \frac{1}{\pi\theta^2} & \|x\| \leq \theta \\ 0 & \text{otherwise} \end{cases}\\ L(\theta) = \prod_{i=1}^n f(X|\theta) = \prod_{i=1}^n \frac{1}{\pi\theta^2}\\ \text{s.t.}\quad \max\|X_i\|\leq \theta$$

log:

$$\ell(\theta) = \ln L = -2n\ln(\frac{1}{\pi})\ln\theta\\\text{s.t.}\quad \max\|X_i\|\leq \theta$$

$\max \;\ell$ we get:

$$\hat\theta = \max(\|X_i\|)$$

6

(1)

Using naive Bayes classifier

$$P(y=1) = \frac{3}{5}\\ P(y=0) = \frac{2}{5}\\ P(x_1 = 1| y=1) = \frac{2}{3}\\ P(x_1 = 1| y=0) = \frac{1}{2}\\ P(x_2 = 1| y=1) = \frac{1}{3}\\ P(x_2 = 1| y=0) = \frac{1}{2}\\ P(x_3 = 0| y=1) = 0\\ P(x_3 = 0| y=0) = \frac{1}{2}\\ P(x_4 = 1| y=1) = \frac{2}{3}\\ P(x_4 = 1| y=0) = \frac{1}{2}\\$$

$$\begin{aligned} P&\{y=1|x=(1,1,0,1)\} \\ &=\frac{1}{p(x)}p(y=1)P(x_1 = 1| y=1)P(x_2 = 1| y=1)P(x_3 = 0| y=1)P(x_4 = 1| y=1)\\ &=\frac{1}{p(x)}\cdot \frac{3}{5}\cdot\frac{2}{3}\cdot\frac{1}{3}\cdot0\cdot\frac{2}{3}\\&=0 \end{aligned} \\ \begin{aligned} P&\{y=0|x=(1,1,0,1)\}\\ &=\frac{1}{p(x)}P(y=0)P(x_1 = 1| y=0)P(x_2 = 1| y=0)P(x_3 = 0| y=0)P(x_4 = 1| y=0)\\ &=\frac{1}{p(x)}\cdot\frac{2}{5}\cdot\frac{1}{2}\cdot\frac{1}{2}\cdot\frac{1}{2}\cdot\frac{1}{2}\\ &=\frac{1}{p(x)}\frac{2}{5} \end{aligned}$$

(2)

经过Laplacian Correction：

$$P(y=1) = \frac{4}{7}\\ P(y=0) = \frac{3}{7}\\ P(x_1 = 1| y=1) = \frac{3}{5}\\ P(x_1 = 1| y=0) = \frac{2}{4}\\ P(x_2 = 1| y=1) = \frac{2}{5}\\ P(x_2 = 1| y=0) = \frac{2}{4}\\ P(x_3 = 0| y=1) = \frac{1}{5}\\ P(x_3 = 0| y=0) = \frac{2}{4}\\ P(x_4 = 1| y=1) = \frac{3}{5}\\ P(x_4 = 1| y=0) = \frac{2}{4}\\$$

$$\begin{aligned} P&\{y=1|x=(1,1,0,1)\} \\ &=\frac{1}{p(x)}p(y=1)P(x_1 = 1| y=1)P(x_2 = 1| y=1)P(x_3 = 0| y=1)P(x_4 = 1| y=1)\\ &=\frac{1}{p(x)}\cdot \frac{4}{7}\cdot\frac{3}{5}\cdot\frac{2}{5}\cdot\frac{1}{5}\cdot \frac{3}{5}\\ &=\frac{0.016}{p(x)} \end{aligned} \\ \begin{aligned} P&\{y=0|x=(1,1,0,1)\}\\ &=\frac{1}{p(x)}P(y=0)P(x_1 = 1| y=0)P(x_2 = 1| y=0)P(x_3 = 0| y=0)P(x_4 = 1| y=0)\\ &=\frac{1}{p(x)}\cdot\frac{3}{7}\cdot\frac{2}{4}\cdot\frac{2}{4}\cdot\frac{2}{4}\cdot\frac{2}{4}\\ &=\frac{0.026}{p(x)} \end{aligned}$$

7

(1)

Bayes网络 $B=<G,\Theta>$ 将属性 $x_1,\ldots,x_d$ 的联合概率分布定义为：

$$P_B(x_1,\ldots,x_d) = \prod_{i=1}^d P_B(x_i|\pi_i) = \prod_{i=1}^d \theta_{x_i|\pi_i}$$

其中 $\pi_i$ 为属性 $x_i$ 在结构 $G$ 中的父节点集， $\theta_{x_i|\pi_i} = P_B(x_i|\pi_i)$ 为每个属性的条件概率表。

联合概率分布：

$$P(x_1,\ldots,x_7) = P(x_1)P(x_2)P(x_3)P(x_4|x_1,x_2,x_3)P(x_5|x_1,x_3)P(x_6|x_4)P(x_7|x_4,x_5)$$

(2)

若观测到 $x_4$ 或 $x_6$ 或 $x_7$的状态，则$x_1, x_2$不相互独立。若对于 $x_4,x_6,x_7$状态未知，则$x_1, x_2$相互独立。

(3)

是独立的。使用 D-Seperation 方法，构造道德图，发现去除 $x_4$ 后， $x_6$ 与 $x_7$ 分属独立分支。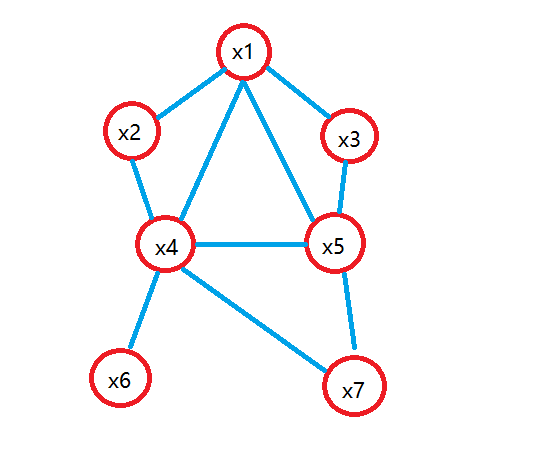

8

(1)

里程：

高	0.5
低	0.5

里程\引擎	好	差
高	0.5	0.5
低	0.75	0.25

空调：

可用	0.625
不可用	0.375

车的价值：

引擎	空调	高	低
好	可用	0.75	0.25
差	可用	0.22	0.77
好	不可用	0.6	0.4
差	不可用	0	1

(2)

若车的价值未知，则引擎与空调独立，有：

$$\begin{aligned} P(\text{引擎=差},\text{空调 = 不可用}) &= P(\text{引擎=差})P(\text{空调 = 不可用}) \\ &= [P(\text{引擎=差}|\text{里程=高})P(\text{里程=高})+P(\text{引擎=差}|\text{里程=低})P(\text{里程=低})]P(\text{空调 = 不可用})\\ &= [0.5 \times 0.5 + 0.25 \times 0.5 ]0.375 \\ &= 0.14 \end{aligned}$$