Machine Learning Homework

1

(1)

主成分分析关键步骤在确定投影矩阵用来压缩维度。在确定投影矩阵过程中选取特征值大的特征向量，而丢弃了特征值小的特征向量。这些向量影响较小，往往与噪声有关。对它们的适当丢弃能对数据降噪。

(2)

主成分分析中对协方差矩阵 $XX^T\quad X \in \R^{D\times N}$ 做特征值分解. $XX^T$ 与 $X^TX\in N\times N$ 有相同的非零特征值的个数，都小于等于 $N$ 。舍去一个最小的特征值得到不超过 $N-1$，即影空间维数不超过 $N-1$

(3)

import numpy as np
X = np.matrix([[2,3,3,4,5,7],[2,4,5,5,6,8]])
print("X:",X)
X1 = X@X.T
print("\nXX^T:",X1)

eigen_values,eigen_vectors = np.linalg.eig(X1)

print("\neigen values:\n",eigen_values)
print("\neigen vectors:\n",eigen_vectors)
#keep the bigger eigenvalue  281

W = eigen_vectors[1]
print("\nW:",W)

new_X = W @ X
print("\nnew X:",new_X)

output:

X: [[2 3 3 4 5 7]
 [2 4 5 5 6 8]]

XX^T: [[112 137]
 [137 170]]

eigen values:
 [  0.96429027 281.03570973]

eigen vectors:
 [[-0.7768816  -0.62964671]
 [ 0.62964671 -0.7768816 ]]

W: [[ 0.62964671 -0.7768816 ]]

new X: [[-0.29446977 -1.21858625 -1.99546785 -1.36582114 -1.51305603 -1.8075258 ]]

2

使用主成分分析的方法可以得到

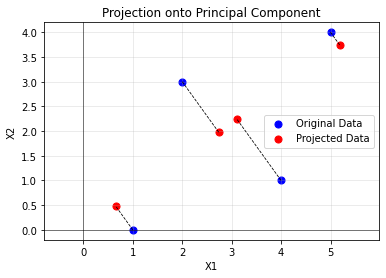
3

第一个为kNN，当k比较小的时候。如果k非常大有可能变为图三。

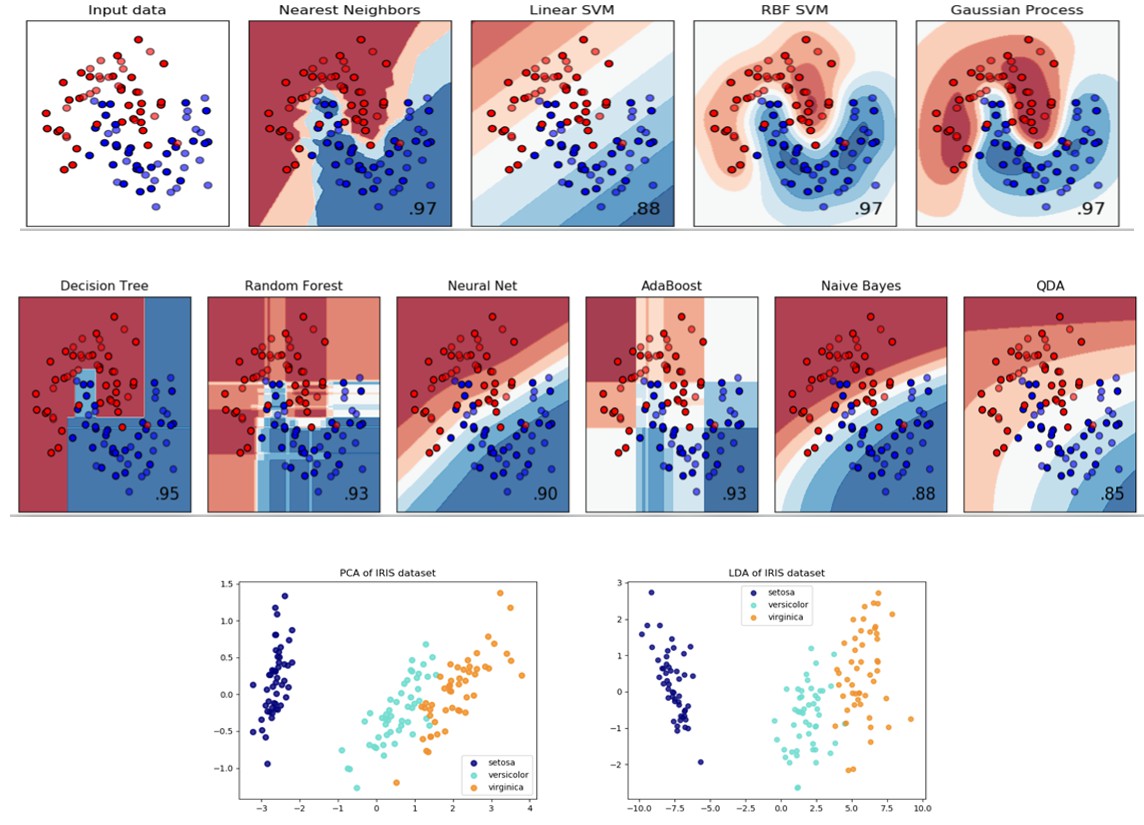
4

ABCD，应该都能用。它们都是分类算法。如果对高维文本数据做好embedding应该都能用。

5

Ridge 使用 $L_2$ 范数 , Lasso 使用 $L_1$ 范数。Lasso跟适合特征选择，因为它将部分协方差置为0，而Ridge不会。但是Ridge可微，Lasso不可微。