Computer Vision

《计算机视觉》课程技术报告（3）

摄像机模型

摄像机模型 Camera Model 描述了一个光路映射坐标的数学模型。模型概括为将三维世界中的立体模型所发出的光线通过光学元件投影成为二维的图像的数学化。

$$s[x',y',1]^T = K[R,T][x,y,z,1]^T$$

其中 $x,y,z$ 为三维坐标，$(x',y')$ 为平面上的点，$K$ 为参数矩阵，与小孔有关。$R，T$ 为外参矩阵，与摄像机的旋转和平移有关。$s$ 为尺度因子。

针孔摄像机模型

针孔摄像机模型pinhole camera model来源于简单的物理学光路原理，是最基本的摄像机模型。假设摄像机主体为小孔，光线通过小孔投影到平面上。

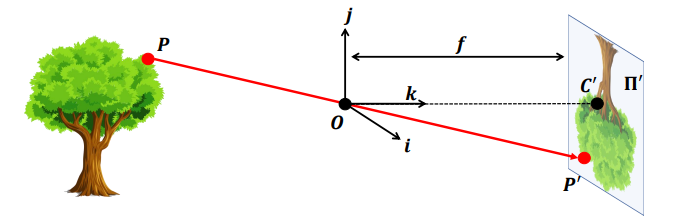
在这种结构中，胶片通常称为像或视网膜平面。光圈称为针孔 O 或相机中心。图像平面和针孔 O 之间的距离是焦距 f。有时，视网膜平面位于 O 和 3D 物体之间，与 O 的距离为 f。在这种情况下，它被称为虚拟图像或虚拟视网膜平面。模型满足公式：

$$[x',y'] = \left[f\frac x z, f\frac y z\right]$$

从几何光学角度出发，当小孔不再足够小后，光先不再满足都通过一个小点的条件，这就导致图像产生虚化直到完全消失。但是从傅里叶光学的角度出发，太小的孔会让光的粒子性减弱而表现为波，造成衍射效应增强。所以并不是孔径越小越好。

透镜模型

现代相机中一般都采用了多种透镜的组合代替以上的小孔。这些透镜通过某种组合仍然满足所有由同一点发出的光线最终都达到像平面上同一点。

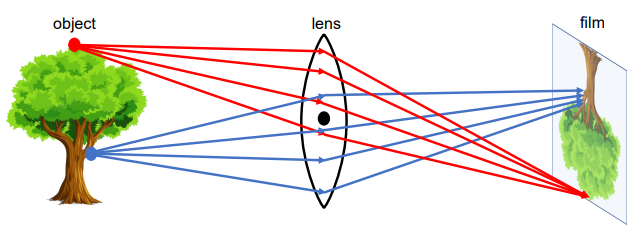
对于一般简单透镜，将所有平行入射光汇聚到的一点称为焦点 ，焦点到透镜中心的距离称为 焦距 。类比针孔模型，可以给出数学建模：

$$[x',y'] = [z' \frac x z , z' \frac y z]$$

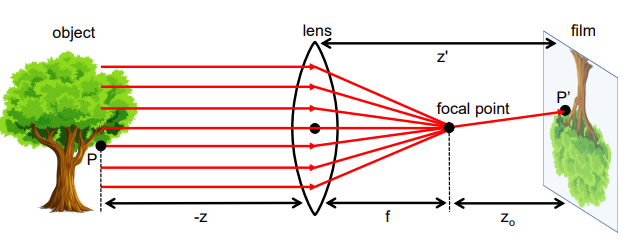
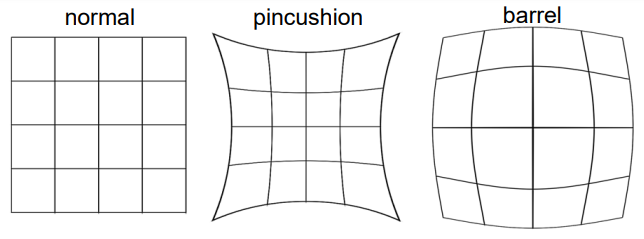
以上模型假设了透镜足够薄且光学性能足够良好。径向畸变由于透镜不同位置焦距不同导致。

数学模型

摄像机的矩阵模型，引入齐次坐标。假设三维空间中点的坐标为 $P = (x,y,z,1)$ , 像点 $P' = (x' ,y' ,1)$

$$P' = \begin{bmatrix} \alpha &0 &c_x &0\\ 0 &\beta &c_y &0\\ 0 &0 &1 &0 \end{bmatrix} \begin{bmatrix} x\\ y\\ z\\1 \end{bmatrix} = K \begin{bmatrix}I &0\end{bmatrix}MP$$

其中 $K$ 矩阵称为 摄像机矩阵 ，$c_x ,c_y$ 为像的偏差，是真实坐标和摄像机像素真实坐标之差。 $\alpha = fk, \beta = fl$。 $l,k$ 为两个方向的像素密度。

$$K = \begin{bmatrix} x'\\ y'\\ z'\end{bmatrix} = \begin{bmatrix} \alpha &-\alpha \cot\theta &c_x \\ 0 &\frac{\beta}{\sin \theta} &c_y \\ 0 &0 &1 \end{bmatrix}$$

建立真实坐标与相机坐标的关系：

$$P = \begin{bmatrix} R&T\\ 0 &1\end{bmatrix}P_w$$

其中$R$ 为旋转矩阵，它是一个正交矩阵 $R^TR = I$ 。 $T$ 为平移矩阵。
对于世界坐标下为 $P_w$ 的点在相机坐标下为 $P$ .
将其代入上面公式，最终得到齐次坐标下的摄像机模型：

$$P' = K\begin{bmatrix}R &T\end{bmatrix}P_w$$

另外由于透镜质地原因，透镜可能并不是处处焦距相等造成径向畸变，透镜安装可能有偏差造成非对称性，称为切向畸变。可以使用多项式描述径向畸变：

$$x_d = x(1 + k_1r^2 + k_2r^4 + \dots)\\y_d = y(1 + k_1r^2 + k_2r^4 + \dots)$$

其中$x_d, y_d$ 为径向畸变后的坐标，多项式系数称为畸变参数，$r^2 = x^2 +y^2$。于是实际坐标$x_a, y_a$ 满足：

$$x_a = \alpha x_d +c_x\\y_a = \beta y_d + c_y$$

图像的成像原理

光学元件

上文从数学的角度简单分析两种光路的数学模型，实际上现代摄像机中通过多种透镜组合，反射，折射，镀膜，滤镜等技术远复杂于以上简单模型。且在不同摄像机中差异巨大，下面只做简单讨论。

1. 反射
   广泛应用于反射镜头和折射镜头中，通过多次反射将光线聚焦到感光元件上。对于如长焦、天文望远镜而言焦距较长而摄像机体积受限，通过反射达到增长光路的效果。反射能避免色差问题因其不依赖于光的波长。
2. 折射
   折射描述光线通过不同折射率的介质时发生传播方向的变化。现代镜头通过对透镜的设计控制球差、色差、畸变等。
3. 镀膜
   镀膜是镜片表面的超薄光学图层，用以减少反射光增加透光率，降低炫光、鬼影等现象。不同成分的镀膜还能对不同波长的光有不同的效果，优化图像质量。
4. 滤镜
   滤镜是在光路中的改变光的特性的光学元件。偏振滤镜 控制光的偏振方向，以减少散射光，提高画面的清晰度。 ND滤镜 降低光的强度，适合在强光或者长曝光等条件下使用。 UV滤镜 又称紫外滤镜阻隔紫外线，提高画面清晰度。颜色滤镜 控制整体画面色彩平衡，提供“氛围感”，或者过滤颜色实现黑白画面。

传感器

现代摄像机主要使用 CMOS队列传感器，简称CMOS。它是一种半导体有源像素传感器，每个光电传感器将光信号转化为电信号输入主板。光线到达像素后经过微透镜聚焦、通过颜色滤镜筛选颜色后进入光电二极管发生光电效应，将光强度转化为电信号。对于每个光电传感器，其只能得知对应颜色光的强度，即光强。计算机将会记录光强为一个灰度值。值的数字精度由图像位深决定。对于jpg图像采用RGB三种颜色排列，使用一个8位二进制数存储每个颜色的数值，即每个像素的一个颜色有256种情况。

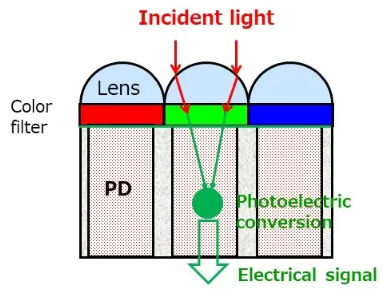
颜色滤镜的排列称为颜色滤光阵列，它决定整体CMOS上的排布。不同摄像机厂商拥有各自的商业方案。一般采用Bayer方案，即每个像素只感知一种颜色的光。

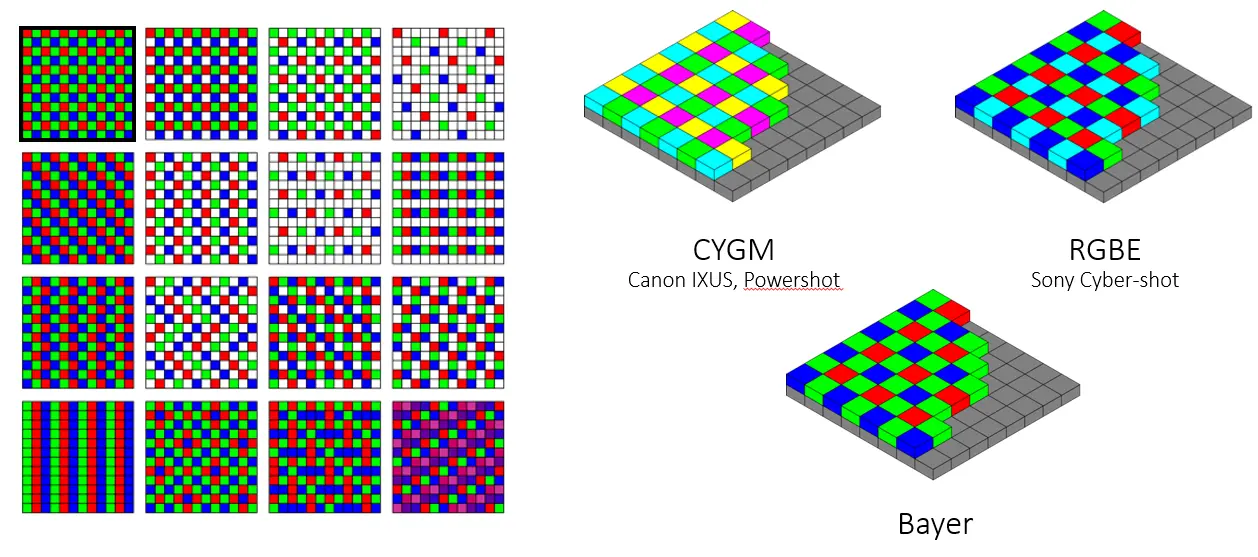
信号处理

获取到电信号后摄像机主板对其进行信号处理得到数字信号。一般摄像机会经过多重算法得到最终数字图像文件，它们有：渐晕处理、白平衡、去马赛克、降噪、伽马校正、色彩空间变换、动态范围调整、畸变校正、裁剪缩放、压缩输出。

1. 渐晕处理
   由于相机的物理结构，图像周围的亮度会暗于图像中心亮度。为此需要对周围像素进行数值补偿。
2. 白平衡
   由于不通拍摄环境光源颜色不通、传感器使用的工艺材料不同等，RGB三个通道的电信号数据有较大差别。相机需要通过白平衡确保输出的颜色和肉眼观察到的颜色相似。基于自然世界假设的白平衡算法是假设图像中最亮的区域为白色。

   $$\begin{bmatrix}R'\\ G'\\ B'\end{bmatrix} = \begin{bmatrix}G_{\max}/{R_{\max}} &0 &0\\ 0 &1 &0\\ 0 &0 &{G_{\max}}/{B_{\max}}\end{bmatrix}\begin{bmatrix}R\\ G\\ B\end{bmatrix}$$

3. 去马赛克
   摄像机获得的原始数据只包含对应像素的对应颜色的数值，而没有其它颜色的数值。使用插值算法依赖旁边像素的颜色数值获得此像素的颜色数值，最终获取完整的RGB三通道信息。
   
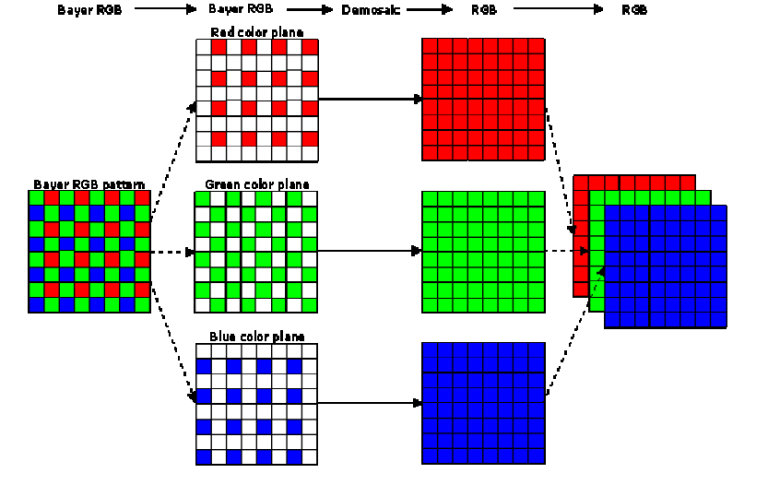
4. 降噪
   由于信号存在噪声，可以使用降噪算法如均值滤波和中值滤波算法降噪。对于每一个像素的值取周围像素的均值或中值进行加权平均。
5. 伽马校正
   调整图片的伽马曲线用来补偿人眼与图像数值的非线性关系。
6. 色彩空间变换
   将传感器的RGB数值转化为计算机颜色空间中的数值，这取决于设定的色彩空间，如sRGB，AdobeRGB等
   
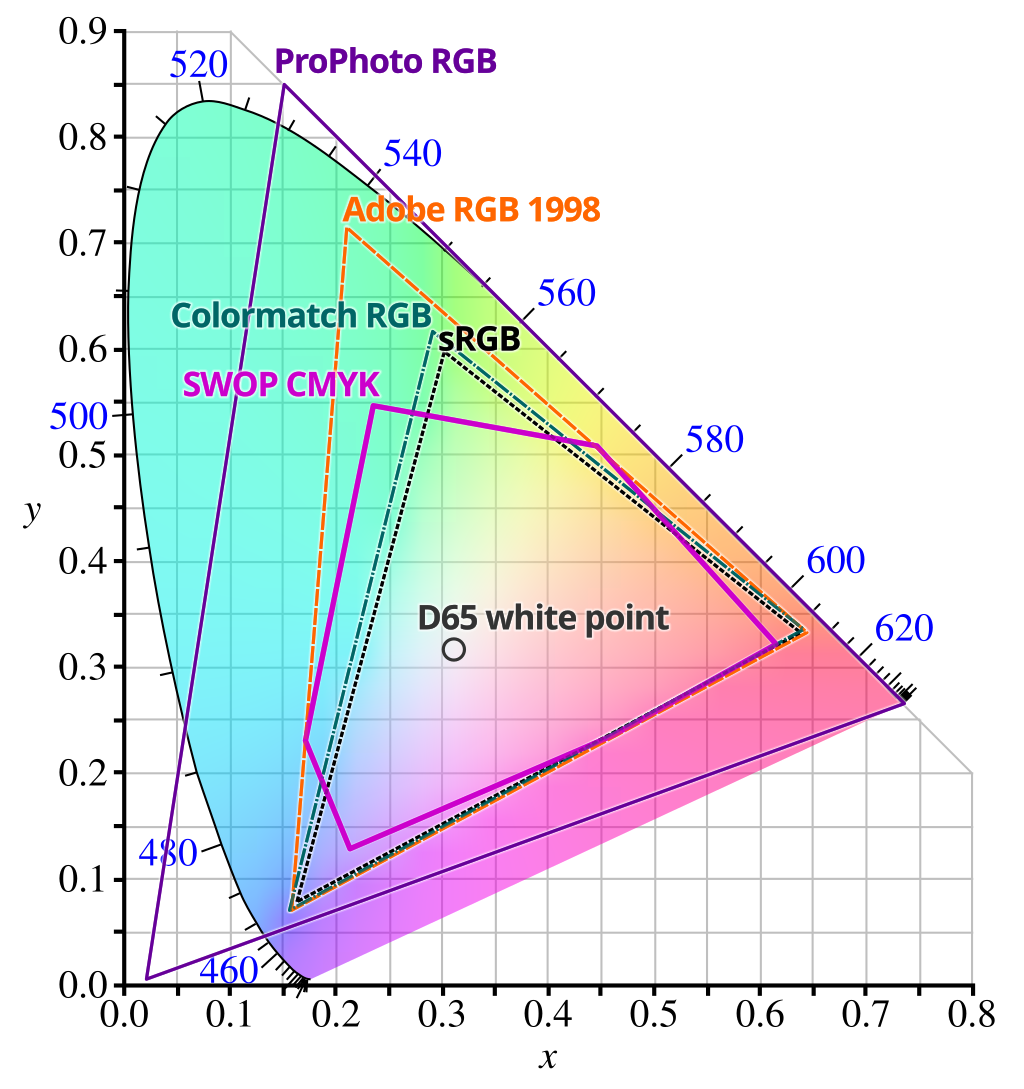
7. 动态范围调整
   现代图像格式存储图像动态范围，根据摄像参数与记录数值计算出真实亮度信息。
8. 畸变校正
   对于广角镜头等可能产生的畸变做几何变换校正
9. 裁剪缩放
   基于用户需求对画面裁剪缩放。对于部分应用场景如视频录制防抖需要裁剪缩放以保持画面稳定清晰。
10. 压缩输出
    根据设定的图像格式压缩原始数据，节省存储空间。或直接输出原始数据文件RAW。