数值分析大作业 Remez 算法
2025年1月9日
算法介绍
Remez算法[2]由苏联数学家 Evgeny Yakovlevich Remez 于1934年提出。这是一个迭代型算法用来求解函数的多项式逼近问题。具体而言,它寻找在Chebyshev空间中 L ∞ L_\infty L ∞ f f f p n p_n p n [ a , b ] [a,b] [ a , b ] a ≤ x 0 < x 1 < ⋯ < x n + 1 ≤ b a\leq x_0<x_1<\cdots<x_{n+1}\leq b a ≤ x 0 < x 1 < ⋯ < x n + 1 ≤ b p n p_n p n f − p n f-p_n f − p n n + 2 n+2 n + 2 p n ( x i ) − f ( x i ) = ( − 1 ) i E p_n(x_i) - f(x_i) = (-1)^i E p n ( x i ) − f ( x i ) = ( − 1 ) i E
算法步骤
初始化节点,通常选取 Chebyshev 节点作为初始猜测。
给定节点组 { x i } i = 1 n + 1 \{x_i\}_{i=1}^{n+1} { x i } i = 1 n + 1 p n ∈ P n p_n\in \mathbb{P}_n p n ∈ P n E E E p n ( x i ) − f ( x i ) = ( − 1 ) i E p_n(x_i) - f(x_i) = (-1)^i E p n ( x i ) − f ( x i ) = ( − 1 ) i E a 0 + a 1 x i + ⋯ + a n x i n − f ( x i ) = ( − 1 ) i E , i = 0 , 1 , … , n + 1 a_0 + a_1x_i+\cdots +a_nx_i^n-f(x_i)=(-1)^i E ,\; i= 0,1,\ldots, n+1 a 0 + a 1 x i + ⋯ + a n x i n − f ( x i ) = ( − 1 ) i E , i = 0 , 1 , … , n + 1
更新节点组:在每个 x i x_i x i p n ( x i ) − f ( x i ) p_n(x_i) - f(x_i) p n ( x i ) − f ( x i ) x ^ i \hat x_i x ^ i
检查停止准则。回到第二步迭代。
停止准则可以使用当最大残差和最小残差的距离小于给定值时停止。也可以使用当新节点与旧节点的差小于某个给定值时停止。另外设置保护准则避免算法无限运行,如最大迭代次数和最长运行时间。n + 2 n+2 n + 2
算法分析
初始节点的影响
初始节点选取 Chebyshev 节点,因为其具有较好的数值稳定性。在多项式插值中,使用Chebyshev节点插值的多项式具有 Lebesgue 常数:
Λ n ( X ) ≤ 2 π log ( n + 1 ) + 1 \Lambda_n(X) \leq \frac 2 \pi \log(n+1)+1
Λ n ( X ) ≤ π 2 log ( n + 1 ) + 1
在尝试使用等距节点的测试中,发现即使在n n n
计算复杂度
第二步解线性系统问题:
a 0 + a 1 x i + ⋯ + a n x i n − f ( x i ) = ( − 1 ) i E , i = 0 , 1 , … , n + 1 a_0 + a_1x_i+\cdots +a_nx_i^n-f(x_i)=(-1)^i E ,\; i= 0,1,\ldots, n+1
a 0 + a 1 x i + ⋯ + a n x i n − f ( x i ) = ( − 1 ) i E , i = 0 , 1 , … , n + 1
通常解一次方程的计算复杂度为 O ( n 3 ) O(n^3) O ( n 3 ) O ( n 2 ) O(n^2) O ( n 2 ) k k k x x x f ( x ) f(x) f ( x ) O ( k n 2 ) O(kn^2) O ( k n 2 )
n n n 测试目标函数:f ( x ) = sin ( x 2 ) + 2 x 2 cos ( 3 x ) f(x)=\sin(x^2)+2x^2 \cos(3x) f ( x ) = sin ( x 2 ) + 2 x 2 cos ( 3 x ) [ − 1 , 1 ] [-1,1] [ − 1 , 1 ] n = 1 , … , 100 n = 1,\ldots, 100 n = 1 , … , 100 n = 1 , … , 11 n = 1,\ldots,11 n = 1 , … , 11 11 < n < 41 11<n<41 11 < n < 41 n > 41 n>41 n > 41
n n n 达到精度
达到最大迭代次数
1~11
0
1
12~40
1
0
41~
0
0
与其他算法的比较
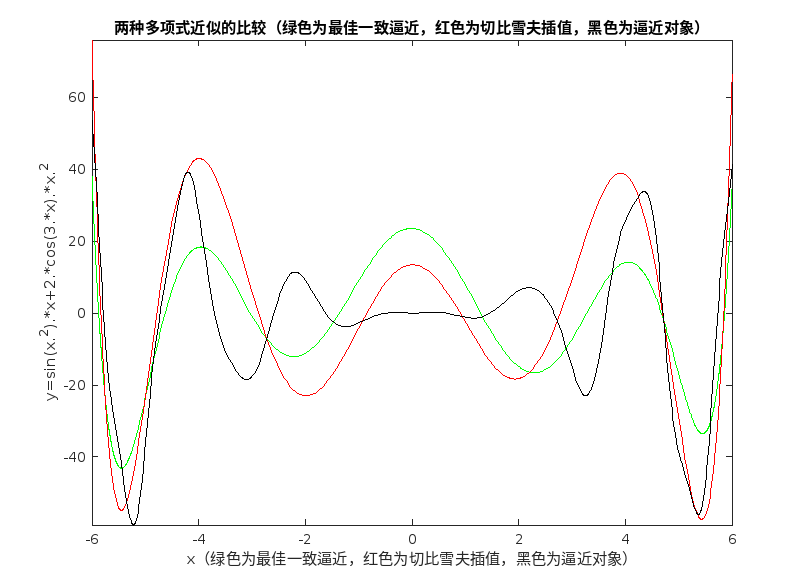
测试目标函数:f ( x ) = sin ( x 2 ) + 2 x 2 cos ( 3 x ) f(x)=\sin(x^2)+2x^2 \cos(3x) f ( x ) = sin ( x 2 ) + 2 x 2 cos ( 3 x ) [ − 6 , 6 ] [-6,6] [ − 6 , 6 ] n = 9 n=9 n = 9
算法
运行时间 (秒)
最大误差
Remez 算法
0.187685
0.145861
插值算法
0.000274
0.223516
目标函数 f ( x ) = e x f(x) = e^x f ( x ) = e x [ − 1 , 1 ] [-1,1] [ − 1 , 1 ]
算法
迭代步数
最佳逼近
Remez 算法
7
0.005571
遗传算法
90
0.005663
插值算法
0.006549
代码实现
输入:f , n , a , b f,n,a,b f , n , a , b
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 function [bestPolynomial, iter] = remesAlgorithm(f, n, a, b, maxError, maxIter)= chebyshevNodes(n+2 , a, b);= 0 ;= inf;<= maxIter) && (error > maxError)= findPolynomial(f, x, n);= @(x) polyval(pCoeffs, x);= @(x) (f(x) - p(x));= findExtrema(g, n, x, a, b);= xNew;= iter + 1 ;= p;= chebyshevNodes(n, a, b)= 1 :n;= cos((2 *k-1 )*pi/(2 *n));= 0.5 *(b-a)*x + 0.5 *(b+a); = findPolynomial(f,x,n)= zeros(n+2 , n+2 );= 1 :n+2 = 1 :n+1 = x(i)^(n-j+1 );1 :n+2 ,n+2 ) = (-1 ).^(0 :n+1 )'; b = f(x)' ;= A\b;= a(1 :n+1 );= findExtrema(f,n,points,a,b)= zeros(1 ,n+2 );= zeros(1 ,n+3 );1 ) = a ; root(n+3 ) = b;= 1 :n+1 3 -i) = findzero(f,points(1 ,i),points(1 ,i+1 ));= 1 :n+2 3 -i) = fminbnd(@(x)-abs(f(x)),root(i),root(i+1 ));= max(f(Extrema))-min(f(Extrema));= findzero(f,a,b)= 1 e-10 ;= (a+b)/2 ;if f(a)*f(x0) < 0 = x0;else = x0;= (a+b)/2 ;
测试:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 = @(x) sin(x.^2 ) + 2 *x.^2 .* cos(3 *x);= -1 ;= 1 ;= 1 e-6 ; = 100 ; = zeros(100 , 2 ); = 1 :40 = remesAlgorithm(f, n, a, b, maxError, maxIter);= linspace(a, b, 1000 );= max(abs(f(xTest) - bestPolynomial(xTest)));if error <= maxError1 ) = 1 ; else 1 ) = 0 ; if iter >= maxIter2 ) = 1 ; else 2 ) = 0 ; 'n | 达到精度 | 达到最大迭代次数' );'-------------------------------' );= 1 :100 '%2d | %9d | %16d\n' , n, results(n, 1 ), results(n, 2 ));1 :100 , results(:, 1 ), 'bo-' , 'DisplayName' , '达到精度' );1 :100 , results(:, 2 ), 'rx-' , 'DisplayName' , '达到最大迭代次数' );'多项式阶数 n' );'结果' );'Remez 算法性能测试' );
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 f = @(x) sin(x) + 0.1 * cos(10 * x);= 9 ;= -6 ;b = 6 ;= 1 e-6 ;= 100 ;= remesAlgorithm(f, n, a, b, maxError, maxIter);= toc;= findInterpolationPolynomial(f,n,a,b);= toc;'Remez 算法的运行时间: %.6f 秒\n' , timeRemez);'插值算法的运行时间: %.6f 秒\n' , timeInterp);= linspace(a, b, 1000 );= max(abs(f(xTest) - bestPolynomialRemez(xTest)));= max(abs(f(xTest) - bestPolynomialInterp(xTest)));'Remez 算法的最大误差: %.6f\n' , errorRemez);'插值算法的最大误差: %.6f\n' , errorInterp);'g' );'r' );'k--' );'Remez 算法' , '插值算法' , '目标函数' );'算法比较' );
参考文献
[1] 数值分析教材.
[2] E.Ya. Remez, Sur le calcul effectiv des polynomes d’approximation des Tschebyscheff,
[3] 张春涛,向瑞银,任友俊.遗传算法在数值逼近中的应用[J].重庆三峡学院学报,2010,26(03):27-29+71.DOI:10.13743/j.cnki.issn.1009-8135.2010.03.041.
[4] 吕致君.最优多项式一致逼近[J].山西大学学报(自然科学版),1980,(01):13-18.DOI:10.13451/j.cnki.shanxi.univ(nat.sci.).1980.01.003.
[5] M.J.D. Powell. Approximation theory and methods. Cambridge University
[6] Wikipedia contributors. “Remez algorithm.” Wikipedia, The Free Encyclopedia. Wikipedia, The Free Encyclopedia, 16 Jul. 2024. Web. 9 Jan. 2025.
[7] de Groot, E. D. (2017). Finding best minimax approximations with the Remez algorithm (Bachelor’s thesis). University of Groningen. Retrieved from https://fse.studenttheses.ub.rug.nl/id/eprint/15985